Table of Contents
Problem definition
The incident field is given as
\( \displaystyle p_{\mathrm{inc}} = \mathrm{e}^{-\mathrm{j} \mathbf{k} \cdot \mathbf{x}} \)
The incident field can be expanded into a series of spherical functions in the \( (r,\theta) \) coordinate frame as
\( \displaystyle p_{\mathrm{inc}}(r,\theta) = \sum_{l=1}^{\infty} (2l+1) \mathrm{j}^{l} j_{l}^{(1)} (kr) P_l(\cos(\theta)) \)
The scatterer is perfectly rigid, i.e., the normal derivative of the sound pressure is zero on its surface \( \displaystyle q = p'_n = 0 \)
\( \displaystyle q_{\mathrm{scat}} = -q_{\mathrm{inc}} \)
The scattered field is found by satisfying the boundary condition and using the spherical expansion of the incident field
\( \displaystyle p_{\mathrm{scat}}(r, \theta) = \sum_{l=0}^{\infty} A_l h_l^{(2)}(kr) P_l(\cos(\theta)) \)
The coefficient \( A_l \) is found as
\( \displaystyle A_l = -(2l + 1) \mathrm{j}^l \frac{l j_{l-1}^{(1)}(kr_0) - (l+1)j_{l+1}^{(1)}(kr_0)}{lh_{l-1}^{(2)}(kr_0) - (l+1)h_{l+1}^{(2)}(kr_0)} \)
Finally, the total sound pressure field is attained as the sum of the incident and scattered fields as
\( \displaystyle p(r, \theta) = p_{\mathrm{inc}}(r, \theta) + p_{\mathrm{scat}}(r, \theta) \)
BEM solution
The BEM solution of the above problem is found by prescribing the scattered velocity field
The infinite sums in series expansions of the incident and scattered fields are truncated up to a given order. To ensure that the error introduced by the truncation is small, the truncated series expansion and the plane wave formula for the incident field are compared and the relative error is evaluated. It is found that it is enough to keep a few tens of terms in the expansion to get a relative error of \( \varepsilon \approx 10^{-7} \).
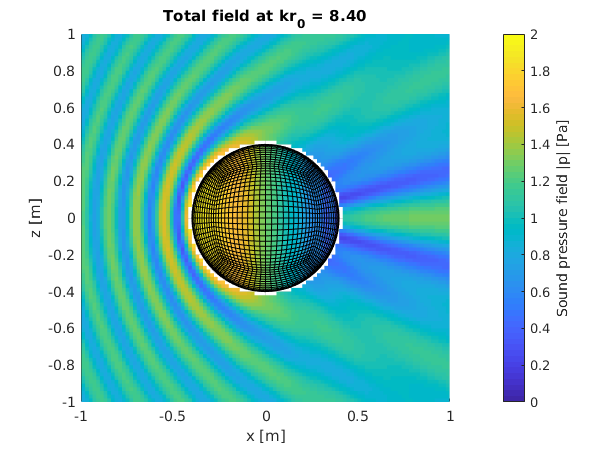
Results
Series truncation error: 1.29315e-07 Surface relative error: 0.0140948 Field relative error: 0.013953
The figure below shows the absolute