Table of Contents
Introduction
This tutorial explains how to use NiHu for evaluating the Rayleigh integral. The Rayleigh integral describes acoustic radiation from an infinite vibrating plane.
In this tutorial, we learn how to connect NiHu with Matlab. The problem geometry and parameters will be imported from, and the results will be passed back to Matlab using NiHu's Matlab interface.
Theory
The Rayleigh integral
The Rayleigh integral computes the acoustic pressure \( p({\bf x}) \) radiated from a vibrating planar surface \( S \) embedded into an infinite rigid plane. The vibrating surface is characterised by its normal velocity function \( v({\bf y}) \). The radiated pressure is evaluated as
\( \displaystyle p({\bf x}) = \int_S G({\bf x}, {\bf y}) v({\bf y}) dS_y = \left(\mathcal{G}v\right)_S({\bf x}) , \)
where \( G \) denotes the fundamental solution of the Helmholtz equation in 3D
\( G({\bf x}, {\bf y}) = \exp(-\mathrm{i}kr)/4\pi r, \quad r = |{\bf y} - {\bf x}| . \)
Discretisation
The velocity field on the surface \( S \) is discretised using piecewise constant or isoparametric interpolation functions:
\( v({\bf y}) = \sum_j w_j({\bf y}) v_j \)
The radiated pressure (the Rayleigh integral) is evaluated in a set of field points \( {\bf x}_i \). For later convenience, we consider the field points as locations in a so called field point domain \( F \). Evaluating the pressure in the field points is equivalent to pre-multiplying the Rayleigh integral with Dirac delta functions located at the field points \( {\bf x}_i \) and integrating with respect to the variable \( {\bf x} \) over the field point domain:
\( \displaystyle p({\bf x}_i) = \sum_j \left(\mathcal{G}w_j \right)_S({\bf x}_i) \cdot v_j = \sum_j \left< \delta_{{\bf x}_i}, \left(\mathcal{G}w_j \right)_S \right>_F \cdot v_j = \sum_j Z_{ij} v_j , \)
where \( Z_{ij} \) denotes the transfer impedance matrix.
Program structure
Our program is organised as follows:
- The two meshes (the radiating surface and the field point mesh) will be generated in Matlab.
- The mesh description matrices (nodes and elements for both meshes) and the wave number \( k \) will be passed to the C++ program from Matlab.
- The C++ program generates the function spaces and evaluates the transfer impedance matrix. The program also computes the radiating surface's radiation impedance matrix that relates the normal velocity to the sound pressure on the surface.
- The transfer and radiation impedance matrices are passed back to Matlab.
The C++ code
Included modules and typedefs
We need three modules from the NiHu library
- core/weighted_residual.hpp is the main module of NiHu
- library/helmholtz_kernel.hpp defines the fundamental solution of the Helmholtz equation
- util/mex_matrix.hpp includes the Matlab interface functions
We further define two typedefs for Matlab matrices NiHu::mex::real_matrix and NiHu::mex::complex_matrix. These matrices are allocated in Matlab's memory, in Matlab format, but are used by NiHu just as if they were C++ Eigen matrices.
The MEX function
Our executable code will be called from Matlab using the syntax
[Z_trans, Z_rad] = rayleigh_integral_3d(surf_nodes, surf_elements, field_nodes, field_elements, wave_number);
The input and output arguments are catched by the C++ function mexFunction
whose parameters are
nlhsthe number of left hand side (output) parameters (two in our case)lhsarray of pointers pointing to the Matlab memory, where the output arguments (Z_transandZ_rad) are allocatednrhsthe number of right hand side input parameters (five in our case)rhsarray of pointers pointing to the Matlab memory, where the five input arguments are allocated
Mesh generation
The radiator surface mesh and the field point mesh is instantiated in C++ as follows:
- The Matlab mesh description matrices are simply imported into C++ by the library class NiHu::mex::real_matrix (
dMatrix). The class' constructor refers to the Matlab input pointer. The resultingdMatrixobjects are light-weight interfaces (views) providing convenient indexing capabilities for the Matlab data.
Function space generation
The function spaces are generated from the two meshes as follows:
- We use an isoparametric function space view of the radiator surface mesh to discretise the velocity field. This means that the velocity nodes are located in the elements' corners, and the velocity is interpolated using linear functions within an element.
- The transfer impedance is evaluated in the element centers of the field point mesh. For this reason, we create a Dirac-view of a piecewise constant function space generated from the field point mesh.
- The radiation impedance is evaluated in the element centers of the radiating surface mesh. For this reason, we create a Dirac-view of a piecewise constant function space generated from the radiating surface mesh.
Kernel and weighted residual
We instantiate the integral operator \( \mathcal{G} \) using the Helmholtz kernel as follows:
- The real wave number is imported from Matlab with the standard Matlab interface function
mxGetPrthat returns a pointer to the real data. - The Helmholtz kernel is instantiated using the class NiHu::helmholtz_3d_SLP_kernel templated to the wave number's type (
double). The abbreviation SLP refers to the single layer potential.
We allocate memory for the output complex matrices:
- The three-argument constructor (rows, columns, output pointer) of class NiHu::mex::complex_matrix (
cMatrix) allocates a Matlab output matrix of given dimensions in Matlab memory.
The weighted double integrals are evaluated using the operator notations:
The two last lines of code are syntactically identical, but there is a great difference.
- The transfer impedance matrix is defined between two separate meshes, and is therefore computed by evaluating regular integrals only
- The radiation impedance matrix is defined on one mesh, so its evaluation involves singular integration.
The complete source of the C++ code is found here: tutorial/rayleigh_integral_3d.mex.cpp
The Matlab code
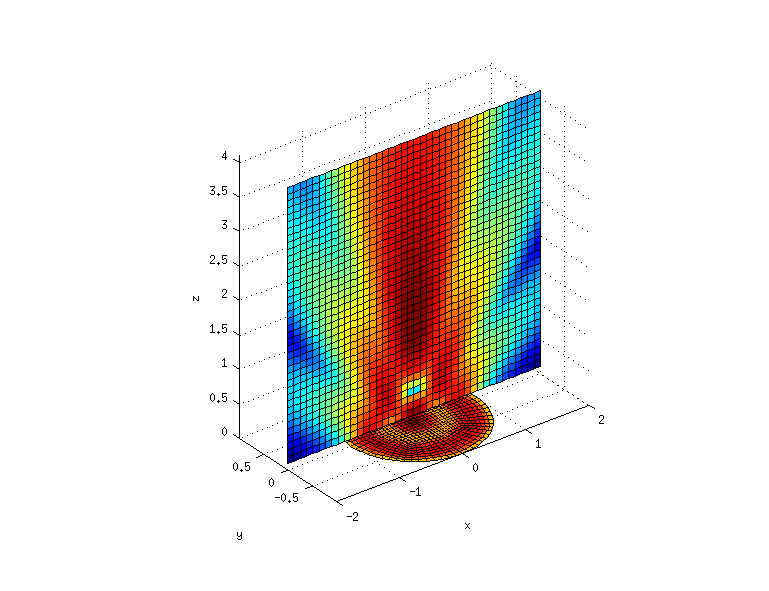
The compiled executable can be called from Matlab, as demonstrated in the example below:
The generated plot looks like