Introduction

This tutorial demonstrates the usage of NiHu for solving an exterior acoustic scattering problem in 2D by means of a collocational type boundary element method (BEM). The modeled problem is scattering of an incident plane wave from a rigid cylinder of radius \(R_0\), centered at the origin of the 2D coordinate system.

Theory

The incident wave field is given as

\( \displaystyle p_{\mathrm{inc}}({\bf x}) = \exp(-\mathrm{i}k {\bf x} \cdot {\bf d}) \)

where \( {\bf d} \) denotes the unit direction vector of propagation. The scattering is considered as superposing a reflected field to the incident pressure field so that the sum of the two fields results a zero velocity on the scatterer surface:

\( \displaystyle p_{\mathrm{tot}}({\bf x}) = p_{\mathrm{inc}}({\bf x}) + p_{\mathrm{ref}}({\bf x}) \\ p'_{\mathrm{tot}}({\bf x}) = 0 \quad {\bf x} \in S \)

This consideration results in the Neumann boundary condition to the reflected wave field:

\( \displaystyle p'_{\mathrm{ref}}({\bf x}) = -p'_{\mathrm{inc}}({\bf x}) \quad {\bf x} \in S \)

The problem is easily formulated with conventional BEM operator notations:

\( \displaystyle q_{\mathrm{ref}} = -p'_{\mathrm{inc}}, \quad {\bf x} \in S, \\ \frac{1}{2} p_{\mathrm{ref}}({\bf x}) = \left(\mathcal{M}p_{\mathrm{ref}}\right)_S({\bf x}) - \left(\mathcal{L}q_{\mathrm{ref}}\right)_S({\bf x}), \quad {\bf x} \in S, \\ p_{\mathrm{ref}}({\bf x}) = \left(\mathcal{M}p_{\mathrm{ref}}\right)_S({\bf x}) - \left(\mathcal{L}q_{\mathrm{ref}}\right)_S({\bf x}), \quad {\bf x} \in F \)

and can be discretised using either collocation or Galerkin formalisms.

Program structure

We are going to implement a Matlab-C++ NiHu application, where

the C++ executable is responsible for assembling the system matrices from the boundary surface mesh and the field point mesh,
the Matlab part defines the meshes, calls the C++ executable, solves the systems of equations, and compares the solutions by quantifying their errors.

The C++ code

The C++ code is going to be called from Matlab as

[Ls, Ms, Lf, Mf] = helmholtz_bem_2d_cyl(...
    surf_nodes, surf_elements, field_nodes, field_elements, wave_number);

Note: The computed surface system matrix Ms will contain the discretised identity operator too, as required by the conventional BEM formalisms.

Header and mesh creation

The header of our C++ source file includes the necessary header files and defines some basic types for convenience. We further include library/helmholtz_singular_integrals.hpp that defines the specialised singular integrals of the Helmholtz kernel for constant lines.

#include "core/weighted_residual.hpp"
#include "util/mex_matrix.hpp"
#include "library/helmholtz_kernel.hpp"
#include "library/helmholtz_nearly_singular_integrals.hpp"
#include "library/helmholtz_singular_integrals.hpp"
 
typedef NiHu::mex::real_matrix<double> dMatrix;
typedef NiHu::mex::complex_matrix<double> cMatrix;

Two meshes will be created, both meshes contain line elements only:

One for the radiator surface (surf_mesh)
One for the field points (field_mesh)

void mexFunction(int nlhs, mxArray *lhs[], int nrhs, mxArray const *rhs[])
{
    dMatrix surf_nodes(rhs[0]), surf_elem(rhs[1]);
    auto surf_mesh = NiHu::create_mesh(surf_nodes, surf_elem, NiHu::line_1_tag());
 
    dMatrix field_nodes(rhs[2]), field_elem(rhs[3]);
    auto field_mesh = NiHu::create_mesh(field_nodes, field_elem, NiHu::line_1_tag());

Definition of function spaces

Next, we create the discretised function spaces of our mesh. The definitions are straightforward, as only constant line boundary elements are dealt with. For the definition of the field point function space, we immediately apply the dirac view.

auto const &surf_sp = NiHu::constant_view(surf_mesh);

auto const &field_sp = NiHu::dirac(NiHu::constant_view(field_mesh));

The number of degrees of freedom on the radiating cylinder \( S \) and in the field mesh \( F \) are denoted by \( n \) and \( m \), respectively. After the function spaces are built, the number of DOFs are known, and the memory for the system matrices can be preallocated. The surface system matrices \( \mathbf{L}_s \), \( \mathbf{M}_s \) are of size \( n \times n \), whereas the matrices describing the field point radiation \( \mathbf{L}_f \) and \( \mathbf{M}_f \) are of size \( m \times n \). The four system matrices are preallocated by means of the following lines of code.

    size_t n = surf_sp.get_num_dofs();
    size_t m = field_sp.get_num_dofs();
    cMatrix Ls(n, n, lhs[0]), Lf(m, n, lhs[2]);
    cMatrix Ms(n, n, lhs[1]), Mf(m, n, lhs[3]);

Integral operators and their evaluation

In the next steps, the three integral operators \( \mathcal{L} \), \( \mathcal{M} \), and \( \mathcal{I} \) are defined. Since the kernel functions depend on the wave number \( k \), which is passed as the fifth right hand side parameter of the mex function, the integral operators are created as follows.

    double k = *mxGetPr(rhs[4]);
    auto I = NiHu::identity_integral_operator();
    auto L = NiHu::create_integral_operator(NiHu::helmholtz_2d_SLP_kernel<double>(k));
    auto M = NiHu::create_integral_operator(NiHu::helmholtz_2d_DLP_kernel<double>(k));

Finally, the system matrices are obtained by the evaluation of the integral operators on the function spaces defined above. Note that as a collocational formalism is applied, the Dirac-view of the test function spaces is taken for the boundary integrals.

    Ls << dirac(surf_sp) * L[surf_sp];
    Ms << dirac(surf_sp) * (M[surf_sp] + (-.5*I)[surf_sp]);
    Lf  << field_sp * L[surf_sp];
    Mf  << field_sp * M[surf_sp];
}

The Matlab code

The example creates a sphere surface of radius \( R = 1\,\mathrm{m} \) centred at the origin, consisting of triangular elements only. The CHIEF points are located on the surface of a cube, shifted from the origin.

The Neumann boundary conditions are defined by a point source located at the point \( \mathbf{x}_0 \). By this definition the geometry is considered transparent, and the resulting acoustic fields on \( S \) are obtained as the acoustic field of the point source.

The compiled mex file can be called from Matlab, as demonstrated in the example below:

%// create meshes
R0 = 1;         %// radius of the cylinder
R1 = 2;         %// radius of the field point mesh
N = 200;        %// number of boundary elements on the cylinder
dir = [1 0 0];  %// direction of the incident plane wave
 
radiator = create_circle_boundary(R0, N);
field_mesh = create_circle_boundary(R1, N);
 
kmax = min(mesh_kmax(radiator));
k = .5 * kmax;
 
%// system matrices
[r_nodes, r_elements] = extract_core_mesh(radiator);
[f_nodes, f_elements] = extract_core_mesh(field_mesh);
[Ls, Ms, Lf, Mf] = helmholtz_bem_2d_cyl(...
    r_nodes, r_elements, f_nodes, f_elements, k);
 
%// Numerical solution
[xs, ns] = centnorm(radiator);  %// center and normal of the cylinder elements
[pinc_s, qinc_s] = incident('plane', dir, xs, ns, k);   %// incident wave field
 
qref_s = -qinc_s;               %// reflected velocity field
pref_s = Ms \ (Ls * qref_s);    %// solution of the BEM problem
ptot_s = pinc_s + pref_s;       %// total pressure field
 
[xf, nf] = centnorm(field_mesh);%// center and normal of the field elements
pinc_f = incident('plane', dir, xf, [], k); %// incident wave field
 
pref_f = Mf * pref_s - Lf * qref_s; %// radiated pressure to field points
ptot_f = pinc_f + pref_f;           %// total pressure in field points
 
%// Analytical solution
pref_f_anal = planewave_cyl2d(xf, R0, k, 100);
ptot_f_anal = pinc_f + pref_f_anal;
 
plot(atan2(xf(:,2), xf(:,1)), abs(ptot_f), '.-', ...
    atan2(xf(:,2), xf(:,1)), abs(ptot_f_anal), '.-');
xlabel('angle [rad]');
ylabel('scattered field');
legend('NiHu', 'Analytic');
 
error = log10(mean(abs(ptot_f./ptot_f_anal-1)));
fprintf(1, 'Log10 mean error: %f\n', error);

The generated plot looks like

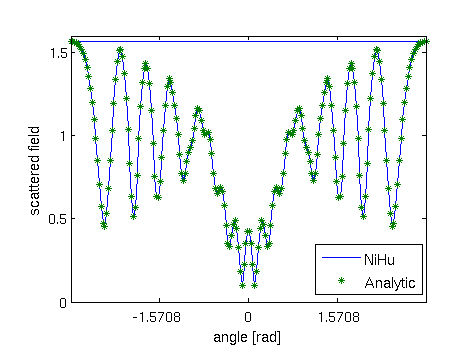
And the resulting errors read as

Log10 mean error: -2.484395

The full codes of this tutorial are available here:

C++ code: tutorial/helmholtz_bem_2d_cyl.mex.cpp
Matlab code: tutorial/helmholtz_bem_2d_cyl_test.m

Table of Contents